JS 中为什么 0.1 + 0.2 != 0.3 ?
昨天在公司大前端做了一次关于计算机怎么计算的分享,顺便研究了一下JS中(严格来说只要是采用IEEE754标准都有这个问题)的精度丢失问题
二进制怎么表示浮点数?
根据IEEE754标准定义了浮点数
单精度(32位):第1位为符号位,第2~9位为指数位,剩余23位为小数位
双精度(64位):第1位为符号位,第2~12位为指数位,剩余52位为小数位
在JS中采用的是双精度浮点数,所以不管是整数还是小数在JS中都是双精度的浮点数

- 第1位符号位:0表示正;1表示负
- 第2~12位指数位:(指数偏移量:2^(11 - 1) - 1 = 1023) 即指数可表示的范围为[-1023, 1024]
- 剩余52位小数位:因为最终的二进制会转成科学记数法,所以整数位始终都是“1”忽略不计,即能表示的最大数为2^(52 + 1) - 1 = 9007199254740991 (在JS中超过这个数就会出现精度丢失问题,下面也会介绍)
JS中的Number
拿圆周率来举个例子
- 圆周率:
Math.PI = 3.141592653589793 - 转换成二进制为:
11.0010010000111111011010101000100010000101101000101111101… - 转换成科学记数法为:
1.10010010000111111011010101000100010000101101000101111101… * 10 ^ 1
因为小数部分只能存储52位,所以只能截取小数位的前52位,舍弃的部分就出现了进位问题,在10进制中一般采用四舍五入,这里采用的是1进0舍 - 所以圆周率最终表示为:
1.1001001000011111101101010100010001000010110100011000 * 10 ^ 1 - 小数部分不变:
1001001000011111101101010100010001000010110100011000 - 指数部分:偏移量+实际指数:
1023 + 1转成二进制为:10000000000 - 符号位:正为 0

现在来看看为什么 0.1 + 0.2 != 0.3 的问题
- 0.1 转成二进制为:0.000110011001100110011001100110011001100110011001100110011001… 其中加粗的部分为小数位,即为: 0.00011001100110011001100110011001100110011001100110011010 精度丢失1次
- 0.2 转成二进制为: 0.001100110011001100110011001100110011001100110011001100110011… 其中加粗的部分为小数位,即为: 0.0011001100110011001100110011001100110011001100110011010 精度丢失1次
- 将两个二进制结果进行求和为: 0.01001100110011001100110011001100110011001100110011001110 最后结果为: 0.010011001100110011001100110011001100110011001100110100 可以看到精度再次丢失
- 三次精度丢失并且都是进位,可以猜出结果会大于 0.3
- 最后将结果转成十进制可以得到:0.30000000000000004
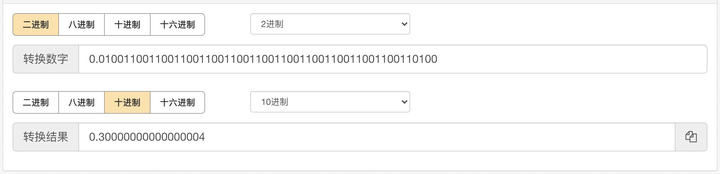
既然0.1 转成二进制精度丢失了,最终还会等于它自身吗?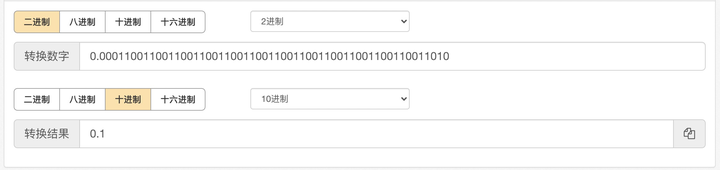
通过转换我们会发现结果还是 0.1 这是为什么呢?
借助高精度转化一下 0.1 会发现我们看到的0.1实际并不是0.1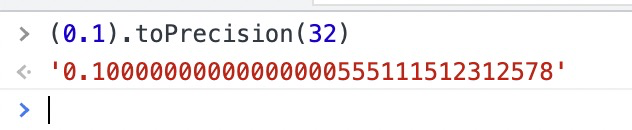 因为小数部分能表示的最大数为 2^52 = 4503599627370495 即最多能表示16位有效数字
因为小数部分能表示的最大数为 2^52 = 4503599627370495 即最多能表示16位有效数字
0.10000000000000000555111512312578 后面的会直接丢掉,你可能会问:为什么“0”后面的“5”没有四舍五入,在这里只是粗略的计算,实际需要转成二进制之后进行舍弃 
再来看一下有意思的现象:
我们知道 toFixed 方法使用定点表示法来格式化一个数值,采用的是四舍五入的方法进行格式化的,但是在遇到精度问题的时候结果可能和你想象的不一样了
举个例子:
(1.335).toFixed(2) // '1.33'当我们放大一下精度就知道原因了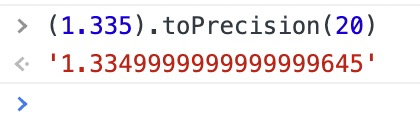
如何解决小数精度丢失的问题?
- 小数取整
即采用最小单位:例如金额不用元而用分(0.1元 = 10分) - 先升再降
即转成整数计算之后再转成小数,可以借用第三方库 number-precision
大数精度丢失问题
现在来推导一个有意思的现象
假如将52位小数位全部填上最大值“1” 并将指数位变为“52”
即:53个“1” 11111111111111111111111111111111111111111111111111111
当我们分别去加“1”和“2”时看看会是什么结果
11111111111111111111111111111111111111111111111111111 + 1 = 100000000000000000000000000000000000000000000000000000 其中加粗部分为52位有效位,最后一位被舍弃
11111111111111111111111111111111111111111111111111111 + 2 = 100000000000000000000000000000000000000000000000000001 其中加粗部分为52位有效位,最后一位被舍弃,这时候可以看到精度丢失了
11111111111111111111111111111111111111111111111111111 + 3 = 100000000000000000000000000000000000000000000000000010 其中加粗部分为52位有效位,最后一位被舍弃
11111111111111111111111111111111111111111111111111111 + 4 = 100000000000000000000000000000000000000000000000000011 其中加粗部分为52位有效位,最后一位被舍弃,这时候可以看到精度丢失了
11111111111111111111111111111111111111111111111111111对应十进制为 9007199254740991
通过打印我们可以发现 +2 、+4都会造成精度丢失,这就是超过 9007199254740991 之后就会有精度问题 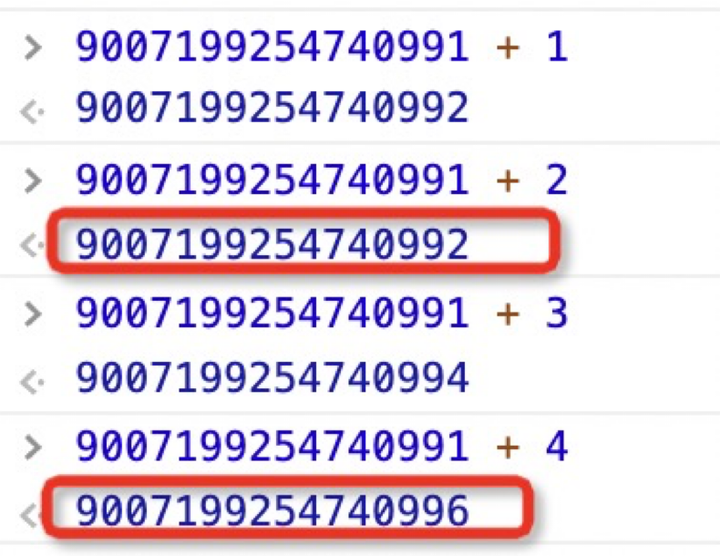
如何解决大数精度问题?
- 数字变字符串处理
- BigInt
结论:
- 只要是采用IEEE754规范的语言都会有精度问题
- BCD编码 用于更高精度的计算
